Matthias Rupp

Machine learning for atomistic systems

Research

Quantum mechanics and machine learning

Stylized representation for QM/ML models

Quantum mechanics (QM), the theory of matter at atomic scale, allows calculation of virtually any property of a molecule or material. However, accurate numerical procedures scale as high-order polynomials in system size, preventing applications to large systems, long time scales, or big data sets. Machine learning (ML) provides algorithms that identify non-linear relationships in large high-dimensional data sets via induction. Our research focuses on models that combine QM with ML. These QM/ML models use ML to interpolate between QM reference calculations, yielding speed-ups of up to several orders of magnitude when the same QM procedure is carried out for a large number of similar inputs, e.g., in virtual screening, molecular dynamics, or self-consistent field calculations. We are particularly interested in models that generalize across chemical compound space.

  • M. Rupp, A. Tkatchenko, K.-R. Müller, O.A. von Lilienfeld: Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning, Physical Review Letters 108(5): 058301, 2012. [doi] [pdf]

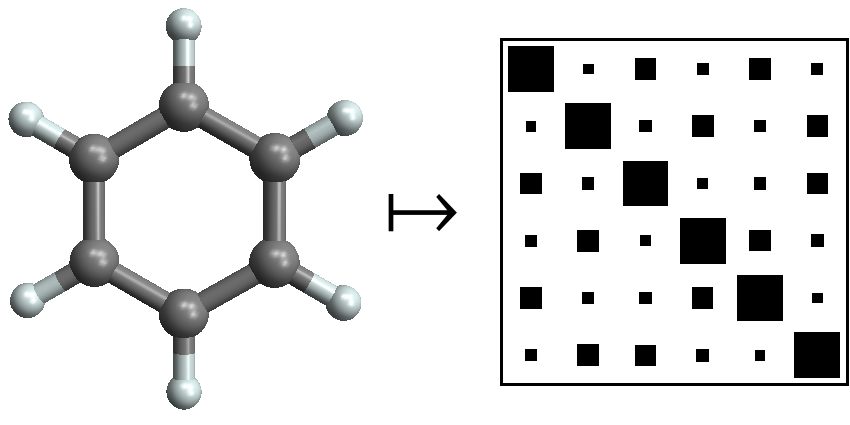
    We use machine learning to predict DFT atomization energies of a diverse set of 7k small organic molecules with an accuracy of 10 kcal/mol, introducing the Coulomb matrix representation to compare different molecules. In follow-up studies, we extend our approach to different properties at various levels of theories, analyzing datasets as large as 134k molecules, and achieving accuracies below 1 kcal/mol.

    1. J.C. Snyder, M. Rupp, K. Hansen, L. Blooston, K.-R. Müller, K. Burke: Orbital-free Bond Breaking via Machine Learning, Journal of Chemical Physics, 139(22): 224104, 2013. [doi] [pdf]
    2. J.C. Snyder, M. Rupp, K. Hansen, K.-R. Müller, K. Burke: Finding Density Functionals with Machine Learning, Physical Review Letters 108(25): 253002, 2012. [doi] [pdf]

    Machine learning is used to estimate the map from electron densities to their kinetic energy in a one-dimensional model potential. With few reference calculations, errors are smaller than typical errors of many exchange-correlation functionals. In follow-up studies, we introduce non-linear gradient denoising to find highly accurate self-consistent densities, successfully dissociating chemical bonds.

Prediction of experimental properties

PPARgamma activator

Reliable computational estimates of experimentally determined properties of small molecules are of high relevance for computer-assisted drug development. Machine learning models of such properties are called quantitative structure-activity/property relationships (QSAR, QSPR), depending on whether the property is biological activity or physico-chemical. We have used tailored kernel-based machine learning methods, including a graph kernel specifically designed for the comparison of small molecules, to develop state-of-the-art QSAR and QSPR models.

    1. M. Rupp, E. Proschak, G. Schneider: Kernel Approach to Molecular Similarity based on Iterative Graph Similarity, Journal of Chemical Information and Modeling 47(6): 2280–2286, 2007. [doi]
    2. M. Rupp, T. Schroeter, R. Steri, H. Zettl, E. Proschak, K. Hansen, O. Rau, O. Schwarz, L. Müller-Kuhrt, M. Schubert-Zsilavecz, K.-R. Müller, G. Schneider: From Machine Learning to Natural Product Derivatives Selectively Activating Transcription Factor PPARγ, ChemMedChem 5(2): 191–194, 2010. [doi]

    We introduce and validate a molecular similarity measure defined directly on the annotated molecular graph, based on iterative graph similarity and optimal assignments. The graph kernel is then used in a combined computational/experimental screening study, resulting in the discovery of a truxillic acid derivative selectively activating transcription factor PPARγ. The compound class is investigated further in follow-up studies.

    1. M. Rupp, R. Körner, I.V. Tetko: Estimation of acid dissociation constants using graph kernels, Molecular Informatics 29(10): 731–740, 2010. [doi]
    2. M. Rupp, R. Körner, I.V. Tetko: Predicting the pKa of small molecules, Combinatorial Chemistry & High Throughput Screening 14(5): 307–327, 2011. [link]

    The biopharmaceutical profile of a compound depends directly on the dissociation constants of its acidic and basic groups. We use kernel-based machine learning and a graph kernel developed earlier to estimate these constants, achieving accuracy comparable to semi-empirical models based on frontier electron theory, but without the need for optimization of structures. For an overview of existing methods for pKa prediction, see reference (b).